Di artikel ini kita akan membahas seputar konsep dari persamaan garis lurus mulai dari pengertian, contoh, bentuk umum persamaan garis lurus, dan cara menentukan apakah suatu persamaan termasuk persamaan garis lurus atau tidak yang juga dilengkapi dengan contoh soalnya.
Sudah siap? Mari kita bahas.
Pengertian Persamaan Garis Lurus
Persamaan garis lurus atau PGL adalah pemetaan persamaan matematika ke dalam bidang kartesius yang membentuk grafik garis linear (lurus).
Intinya, persamaan garis lurus itu adalah persamaan yang kalau digambar, gambar yang terbentuk itu adalah garis lurus.
Emang ada persamaan yang grafiknya nggak lurus?
Ada. Contohnya itu seperti persamaan kurva.
Contoh Persamaan Garis Lurus
Mungkin ada kalian yang bingung, persamaan kurva itu emang bentuknya gimana?
Kalau persamaan garis lurus itu gini
Sedangkan kalau persamaan kurva itu seperti ini
Kelihatan kan bedanya?
Kalau grafik persamaan garis lurus itu gambarnya lurus terus. Sedangkan kalau grafik persamaan yang bukan garis lurus itu ada belok belok nya.
Tapi, kalau tanpa gambar grafiknya, bisa nggak kita mengetahui persamaan tersebut termasuk ke persamaan garis lurus atau tidak?
Bentuk Umum Persamaan Garis Lurus
Bentuk umum persamaan garis lurus adalah
ax + by + c = 0
Ingat ya a dan b adalah koefisien sedangkan c merupakan suatu konstanta.
Selain bentuk di atas, biasanya persamaan garis lurus juga ditulis seperti ini
y = mx + c
dengan m adalah gradien garis sebagai koefisien dan c adalah konstanta.
Apa itu gradien?
Nanti kita bahas.
Cara Menentukan Persamaan Garis Lurus
Kita bisa menentukan apakah suatu persamaan itu termasuk ke persamaan garis lurus atau tidak.
Caranya?
Cukup lihat pangkat variabel x dan y nya.
Jika variabel x dan y nya berpangkat 1, maka persamaan tersebut adalah persamaan garis lurus.
Namun jika variabel x atau variabel y nya berpangkat lebih dari 1, maka persamaan tersebut bukanlah persamaan garis lurus.
Contoh Soal Menentukan Persamaan Garis Lurus
Mari kita bahas contohnya.
Persamaan berikut yang termasuk persamaan garis lurus adalah
A.2y + x² - 10=0
B.4x - 2x - 2=0
C.x²=5y + 2
A. 2y + 4x=0
Kita coba analisis satu per satu.
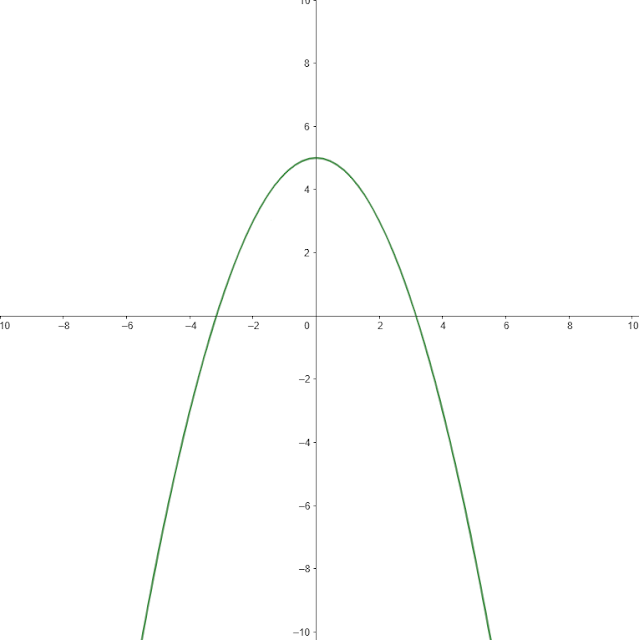
A. 2y + x² - 10=0
Walaupun y nya berpangkat 1, tetapi x nya berpangkat 2. Sehingga persamaan tersebut bukanlah persamaan garis lurus.
Kita coba lihat grafiknya.
Bukan garis lurus kan? Mari kita lanjut bahas selanjutnya
B. 4x - 2x - 2=0
Biar lebih mudah, kita coba sederhanakan dulu persamaannya.
4x - 2x - 2=0
2x – 2 = 0
Mungkin kalian berfikir persamaan ini bukan persamaan garis lurus karena y nya itu nggak ada. Padahalkan tadi syaratnya persamaan garis lurus itu, x dan y nya harus berpangkat 1.
Eits, hati hati.
Persamaan tersebut juga sama seperti ini 2x + (0)y -2 = 0
Sama kan?
Nah, dari sini kita bisa lihat bahwa jika x atau y nya tidak ada, bukan berarti pangkat dari x atau y nya itu adalah 0.
Nah, karena pangkat x dan y nya adalah 1, maka persamaan tersebut termasuk persamaan garis lurus.
Gambar dari persamaan tersebut adalah seperti ini
C. x² = 5y + 2
Yap, karena x nya adalah pangkat 2, maka persamaan tersebut bukan persamaan garis lurus.
Grafik persamaan tersebut seperti ini
D. 2y + 4x=0
Ya, persamaan tersebut adalah persamaan garis lurus karena pangkat x dan y nya adalah 1.
Grafik dari persamaan tesebut adalah seperti ini
Dari persamaan A, B, C, D yang sudah kita analisis tadi, didapatkan kalau persamaan B dan D merupakan persamaan garis lurus.
Intinya, menentukan apakah suatu persamaan termasuk persamaan garis lurus atau tidak sesimpel melihat pangkat x dan y nya saja.
Kesimpulan
Dari artikel ini, kita sudah membahas beberapa seputar persamaan garis lurus, yang poin-poin besarnya itu seperti ini :
- Persamaan garis lurus adalah persamaan yang kalau digambar, hasilnya adalah garis lurus.
- Bentuk umum persamaan garis lurus adalah ax + by + c = 0 dan y = mx + c
- Jika pangkat x dan y nya adalah 1, maka persamaan tersebut adalah persamaan garis lurus.